I was talking to a friend of mine who teaches middle school math this week. It brought back all sorts of memories about my career in math, how I picked my classes over my primary and secondary schooling, and what I would tell my teen-aged self with the benefit of hindsight if such self would actually listen to an adult back then.
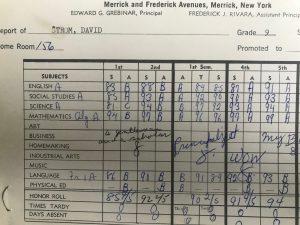 I come from a family of math geeks: my sibs and my parents were all good at math, and all of the kids were on the “math team” that met after school to solve problems and compete for prizes. Looking through my old report cards, rarely did I get a grade less than an A in any of my classes. When it came time for college though, I started out as a physics major, quickly changing to math when I got frustrated with all the prerequisites, and eventually graduating with a roll-my-own major that combined independent study classes in science, art and math.
I come from a family of math geeks: my sibs and my parents were all good at math, and all of the kids were on the “math team” that met after school to solve problems and compete for prizes. Looking through my old report cards, rarely did I get a grade less than an A in any of my classes. When it came time for college though, I started out as a physics major, quickly changing to math when I got frustrated with all the prerequisites, and eventually graduating with a roll-my-own major that combined independent study classes in science, art and math.
What many parents don’t realize until their kids have been through middle school is that there is in most districts a separation of kids into two math tracks. One is the basic math curriculum which involves teaching algebra, trig, geometry and some statistics by the time you finish high school. The other is a more advanced series of classes that ends with students taking calculus in their senior year in high school. If you are good at math, you end up with the latter program of study.
Why does anyone need to study calculus? There really isn’t any good reason. It is more custom than necessity. In my case, getting calculus “out of the way early,” (as I look at it now) allowed me to get AP credit and graduate early from college. It also enabled me to take more advanced math classes too. I asked Arnold Seiken, one of my former college math professors, why anyone should take the class. He was mostly bemused by the question: “Calculus was always part of the requirements for graduation – students assume that it is part of the burden of life and just grin and bear it. I assume you took my courses because you liked the jokes. I can’t think of any other reason.” He was right: he was always a crack-up, in class and now in retirement. Interestingly, he told me that he got into math by accident in high school because he couldn’t do the science labs, much like I decided. “Math was a fallback for me, I was always breaking stuff in the labs.” He was an excellent teacher, BTW.
When you are a college math major, there are basically two different career paths you hear about: to teach or to become an actuary. I wasn’t all that excited about teaching (although I did dabble with teaching both a high school computer class and a graduate business class later on in life), and when I took the first exam of many to become an actuary, I got the lowest possible passing score. That first exam is calculus, and my justification for the miserable score was because I hadn’t had any calculus for several years by the time I took the exam. But it didn’t bode well for a career in that field.
But having plenty of math classes – including one on linear algebra taught by Seiken — also enabled me to have a solid foundation for graduate school study of applied math topics that were part of my degree in Operations Research. That took me to DC and to do math modeling for supporting government policy analysis, and eventually on to general business technology.
 My master’s degree was issued in the late 1970s. Back then we didn’t have personal computers, we didn’t have spreadsheets, we didn’t have data modeling contests like Kaggle. What we did have was a mainframe on campus that you had to program yourself if you wanted to do mathematical models. Today you can use Excel to solve linear programs and other optimization problems, set up Chi Square analyses, run simulations and other things that were unthinkable back when I was in school – not that I would know how to do these things now if you forced me to watch a bunch of videos to relearn them.
My master’s degree was issued in the late 1970s. Back then we didn’t have personal computers, we didn’t have spreadsheets, we didn’t have data modeling contests like Kaggle. What we did have was a mainframe on campus that you had to program yourself if you wanted to do mathematical models. Today you can use Excel to solve linear programs and other optimization problems, set up Chi Square analyses, run simulations and other things that were unthinkable back when I was in school – not that I would know how to do these things now if you forced me to watch a bunch of videos to relearn them.
Seiken reminded me of a part-time job that I had in college, repairing these ancient geometric string models that were used in the 1800s to teach engineering students how to draw conic sections. I didn’t need calculus to restring the models, although it helped to understand the underlying geometry to figure the string placement. It did get me started on my path towards problem-solving though.
And I think that is what I would tell my teenage self. Whether or not I took this or that math class, what I was good at is solving technical problems. Having a math background made it easier for me to pick a more technical career path. Had I not moved into the calculus track, I probably would still have been interested in math of some kind, but probably wouldn’t have been as challenged to take the advanced classes I was doing as a junior and senior in college. So yes, calculus per se isn’t really relevant to debugging a network protocol stack, or figuring out the root cause of a piece of malware, but it does train you to learn how to pick apart these problems and find your way to an answer. Now, your kids may have a different path towards developing their own problem-solving skills, but math was my ticket and I am glad I took the path that I did.
Thanks for your story about the place of calculus in your learning math. I had a somewhat different encounter with calculus. It was a requirement in the structural engineering curriculum at Cal when I was a student in the mid-60s. We were supposed to use it to calculate things like bending stresses in loaded beams. I got a night clerk job at a motel so I would have plenty of uninterrupted quiet time to study, and was part of a group of students who got together to figure out problems. After I survived the course, two things came to light: one was a huge table of predetermined figures for standard size/material beams, that engineering practitioners used for typical structures, the second was an HP calculator that made quick work of the former hand calculations. I have never had to use calculus since school. So my impression is, calculus showed me how to organize an effective approach to a tough situation, to be practical, and be happy for whatever outcome. But when I recently found my course notes in the basement, I realized, looking at my own handwriting, I had no idea what the notes meant. I have erased calculus from my memory.
This is the perfect example of what’s been lost in education. The most important goal of education shouldn’t be to teach you skills and techniques that you will need to get and keep good employment so you can afford to live and raise a family. The goal above all others should be to teach you to learn. Learn how to learn concrete topics and ideas. Learn to learn more abstract philosophical topics and ideas. Learn to recognize what you need to learn. Almost no one enters the work world knowing what they need to know for the job, but hopefully they have learned to be good learners and can quickly learn whats necessary to become a valued employee. What better abstract, out of touch with reality concept to use to push your ability to learn than advanced math topics like calculus. If you can learn that, you can learn almost anything. It was always one of those courses that separated the men from the boys and the educational system needs those courses. We can’t (and shouldn’t want to) make everything easy for everyone. Is eliminating calculus part of our ‘everyone deserves a trophy’ mentality? Should we get rid of courses like this just because it’s hard and almost no one likes it? You can’t claim to be at the top of the heap if there are no challenges to differentiate yourself from others and courses like calculus represent those sorts of challenges.
Interesting, and funny that yourcollege path was same as mine (and a friend from first day college!) — we started as physics majors but after two years recognized the folly in that so switched to math.
But I disagree about your two choices as college math major (teach or actuary); I describe choices I had as graduate school, drive a cab, and computers. Third choice won for me and friend, worked out nicely for us both.
“it (calculus) does train you to learn how to pick apart these problems and find your way to an answer.” To me, that is the first reason to study advanced mathematics. It introduces a mental framework and discipline needed for most any problem solving. Second reason is that calculus and differential equations describe how our physical world works, so I would also advocate for more than a superficial high school study of physics.
My own college career was more contorted than yours, but the study of higher math and computer science provided an excellent foundation for a long career in the computer industry. The other important piece was the study that ultimately lead to a B.A. in English Literature. Now I can write and communicate verbally, but with the logic, most of the time, of one who studied math.
Yes, you are a “gentleman and a scholar”! It is interesting that this was obvious to your advisor in ninth grade! I, too, took AP Calculus in high school and a year of calculus in college. I fell off the bandwagon completely with advanced differential calculus — the only course I ever took in which I was clueless from the get-go! But the two years of successful calculus I did complete surely enhanced my problem-solving and logical thinking, which — as you have known me for 30 years — can always use a boost!